Square root of an integer

Finding the square root of an integer is a common problem in programming, especially when designing algorithms for mathematics, gaming, or simulations. In this blog post, we’ll explore how to compute the square root of an integer efficiently in Java. We will cover various approaches, from the naive method to more optimized algorithms like Binary Search and Newton’s Method.

Problem Statement:

Given an integer N, find its square root. If N is not a perfect square, then return floor(√n).

What is the Square Root?

The square root of a number xxx is a value yyy such that:y2=xy^2 = xy2=x

For example, the square root of 999 is 333, as 32=93^2 = 932=9. When dealing with integers, the square root is typically rounded down to the nearest whole number (floor value) if the result isn’t a perfect square.

Approaches to Find the Square Root

Here are three common methods to calculate the square root of an integer in Java:

1. Naive Approach (Iterative Method)
2. Binary Search Approach
3. Newton’s Method

Let’s dive into each method with explanations and Java code.

1. Naive Approach

In this approach, we iterate through numbers starting from 111 until i2i^2i2 exceeds the target number. The last iii that satisfies i2≤xi^2 \leq xi2≤x is the square root.

Code Example:

public class SquareRootNaive {
    public static int squareRoot(int x) {
        if (x == 0 || x == 1) {
            return x;
        }

        int result = 1;
        for (int i = 1; i * i <= x; i++) {
            result = i;
        }
        return result;
    }

    public static void main(String[] args) {
        int number = 25;
        System.out.println("Square root of " + number + " is " + squareRoot(number));
    }
}

Time Complexity:

• O(√n) as we iterate up to the square root of nnn.

2. Binary Search Approach

Binary Search is an efficient way to calculate the square root, especially for large numbers. The idea is to search within a range [0,x][0, x][0,x], repeatedly narrowing it down based on the square of the mid-value.

Code Example:

public class SquareRootBinarySearch {
    public static int squareRoot(int x) {
        if (x == 0 || x == 1) {
            return x;
        }

        int start = 0, end = x, result = 0;
        while (start <= end) {
            int mid = start + (end - start) / 2;

            if (mid <= x / mid) {
                result = mid; // Mid is a valid candidate
                start = mid + 1;
            } else {
                end = mid - 1;
            }
        }
        return result;
    }

    public static void main(String[] args) {
        int number = 49;
        System.out.println("Square root of " + number + " is " + squareRoot(number));
    }
}

Time Complexity:

• O(log n) due to the binary search process.

3. Newton’s Method

Newton’s Method is an iterative numerical method for finding approximations to the roots of a real-valued function. For finding square roots, the function used is:

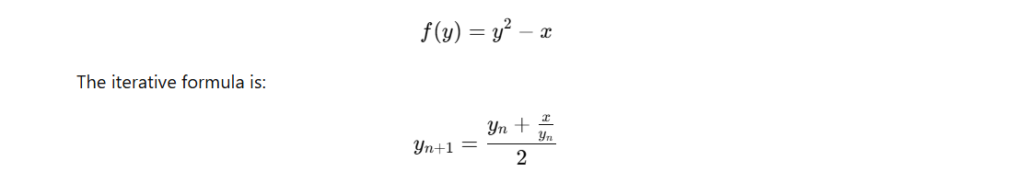
Code Example:

public class SquareRootNewton {
    public static double squareRoot(int x) {
        if (x == 0 || x == 1) {
            return x;
        }

        double guess = x;
        double epsilon = 1e-6; // Precision level
        while (Math.abs(guess * guess - x) > epsilon) {
            guess = (guess + x / guess) / 2;
        }
        return guess;
    }

    public static void main(String[] args) {
        int number = 50;
        System.out.printf("Square root of %d is %.5f%n", number, squareRoot(number));
    }
}

Time Complexity:

• O(log n), as it converges rapidly.

Which Approach Should You Use?

• Naive Approach: Simple and easy to implement, suitable for small numbers.
• Binary Search: Efficient and handles large numbers effectively.
• Newton’s Method: Ideal for high precision but slightly more complex.

Applications of Square Root Calculation

1. Computer Graphics: Used for calculating distances between points.
2. Physics Simulations: Involves calculations for velocity and acceleration.
3. Gaming: Determines collision detection and rendering.
4. Data Science: Used in algorithms like Euclidean distance for clustering.

Conclusion

Calculating the square root of an integer is a fundamental problem in programming. We explored three approaches, each with its own merits and use cases. The Binary Search and Newton’s Method are highly efficient, while the naive method is simple for beginners.

Do you have any other Java coding problems you’d like us to cover? Share your thoughts in the comments below!